7-18 July 2013
Bałtycki Istytut Matematyki,
Gdynia, Poland
Mini-course:
The role of global invariant manifolds in the
organisation of chaotic dynamics
This course is concerned with the global organization of phase space near global bifurcations
of three-dimensional vector fields. Typically, these phenomena cause global re-arrangements
of the dynamics, including the (dis)appearance of periodic orbits, changes to basins of attractions
and the generation of chaotic dynamics. This is of special interest to understand the
nature of systems
near global bifurcations such as in laser dynamics,
nerve impulses in neurons, electrochemical reactions,
communication
systems based on chaos, food chains in predation models, etc.
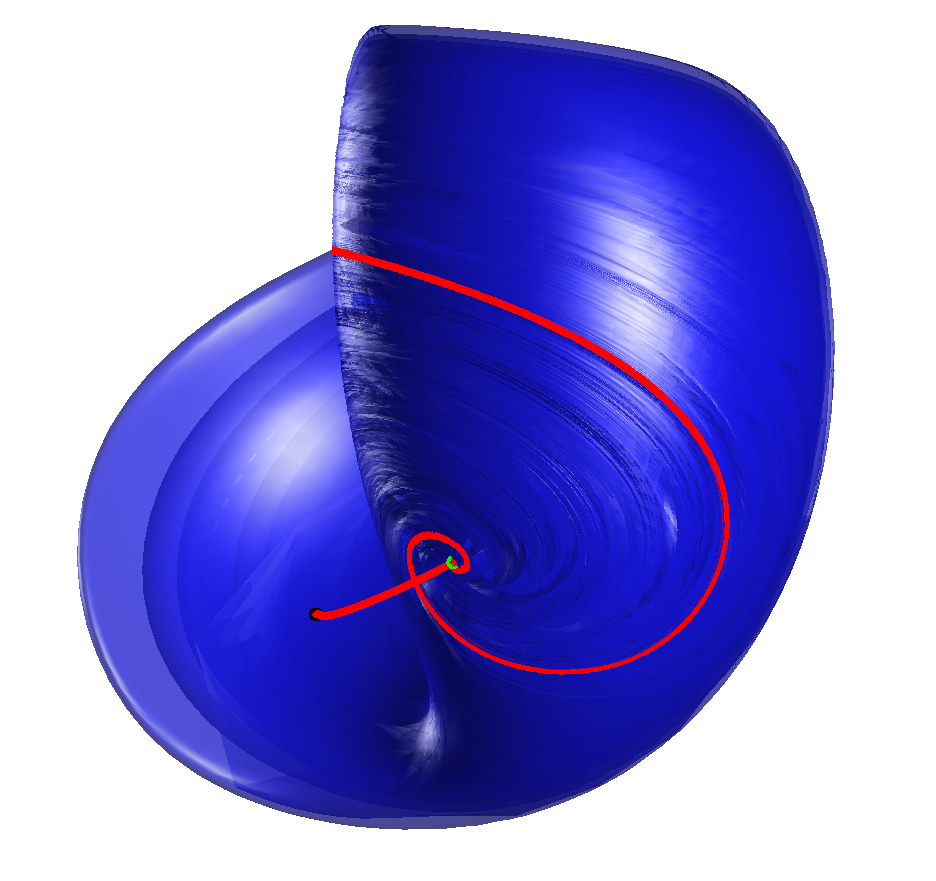
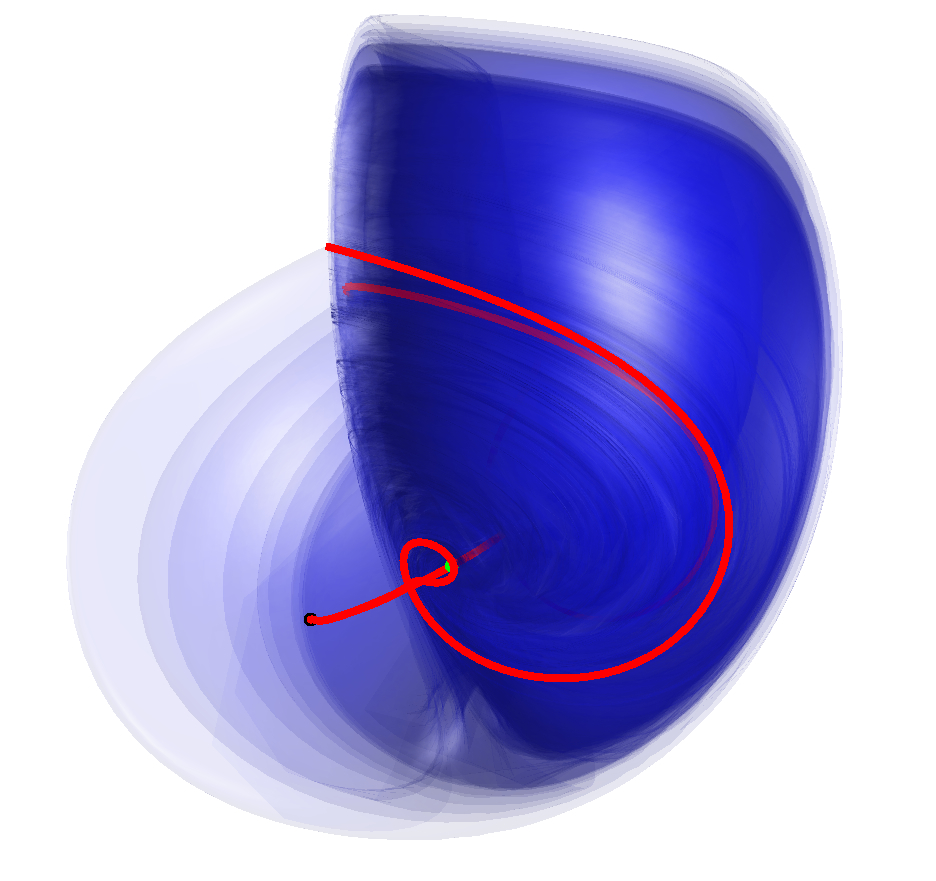

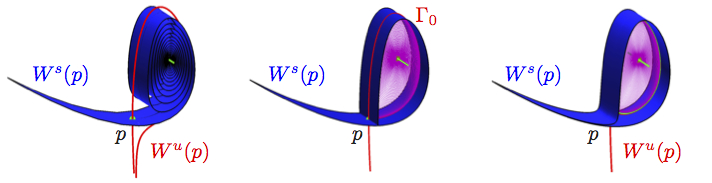
Our approach is to study how the relevant two-dimensional (un)stable manifold rearrange themselves globally
near homoclinic bifurcations to reconfigure the overall organization of the dynamics in phase space.
In order to deal with these questions we make extensive use of analytical tools from dynamical systems theory
in combination with advanced numerical methods for the accurate computation of higher-dimensional global
(un)stable manifolds. More specifically, we compute these manifolds via the numerical continuation of orbit
segments as solutions of a boundary value problem.
This course will focus in three main areas:
1) An introduction on the basic mathematical background: Bifurcations
of vector fields, invariant manifolds of
equilibria and periodic
orbits, routes to chaos, applications.
2) Computational methods: Numerical bifurcation analysis, detection and continuation of homoclinic bifurcations,
computation and visualisation of global invariant manifolds.
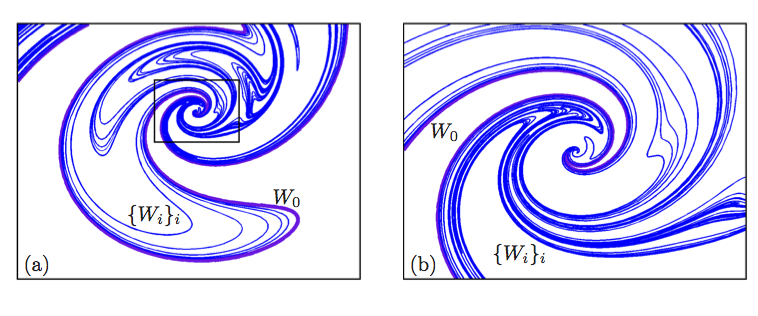
3) An overview of recent research topics: invariant manifolds in the unfolding of codimension-one and codimension-two
homoclinic bifurcations, Shilnikov chaos, the
(non)orientability of a homoclinic bifurcation, the Lorenz manifold,
etc.
All from both theoretical and applied contexts. And future challenges: Bifurcations
to non-hyperbolic equilibria, higher
codimension phenomena, etc.
In this way, we are able to explain how the global
bifurcations of interest may lead to quite dramatic changes of the overall dynamics.
References:
P. Aguirre, E. Doedel, B. Krauskopf and H.~M.~Osinga,
Investigating the consequences of global bifurcations for two-dimensional manifolds of vector fields,
Discrete and Continuous Dynamical Systems - Series A, 29, pp. 1309-1344, 2011.
P. Aguirre, B. Krauskopf and H. M. Osinga,
Global invariant manifolds near a Shilnikov homoclinic bifurcation,
to appear in Journal of Computational Dynamics.
P. Aguirre, B. Krauskopf and H. M. Osinga,
Global invariant manifolds near homoclinic orbits to a real saddle: (non)orientability and flip bifurcation,
to appear in SIAM Journal on Applied Dynamical Systems.
J. Guckenheimer and P. Holmes,
Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields,
Second ed., Springer-Verlag, New York/Berlin, 1986.
Yu. Ilyashenko and W. Li,
Nonlocal Bifurcations,
Mathematical Surveys and Monographs, vol. 66, American Mathematical Society, Providence, RI, 1999.
B. Krauskopf and H. M. Osinga,
Computing invariant manifolds via the continuation of orbit segments,
in Numerical Continuation Methods for Dynamical Systems, Underst. Complex Syst.,
Springer-Verlag, New York, 2007, pp. 117-154.
Yu. A. Kuznetsov,
Elements of Applied Bifurcation Theory,
Third ed., Springer-Verlag, New York/Berlin, 2004.
Universidad
Técnica Federico Santa María
/ Departamento
de Matemática
/ P Aguirre







