Tópicos de investigación
Los sistemas dinámicos son sistemas que
evolucionan con el tiempo, y se encuentran por todas partes:
desde el sistema solar, el clima y los ecosistemas, hasta en
las máquinas creadas por el hombre y en la bioquímica de
nuestros propios cuerpos. Dependiendo de las circunstancias,
el comportamiento de un sistema puede ser bastante simple o
más bien complicado. El modelo de Lorenz ---con su icónico
atractor caótico con forma de alas de mariposa--- es un
ejemplo paradigmático de un sistema dinámico con
comportamiento complicado. Su aparicion hace más de 50 años
fue una de las piedras angulares para el desarrollo de la
teoría moderna de sistemas dinámicos y dio pie al surgimiento
de lo que hoy se entiende por Teoría del Caos.
Mi investigación se focaliza
en entender el rol de ciertos objetos especiales en un sistema
dinámico, llamados variedades
invariantes. Nos enfocamos en el rol de estas
variedades como organizadores de los distintos comportamientos
cualitativos en un sistema dinámico. Estas variedades son
superficies (o hipersuperficies) que actúan como fronteras que
separan diferentes regiones en el espacio de estados de un
sistema. Por ejemplo, trayectorias a un lado de una variedad invariante pueden
evolucionar en el tiempo hacia un comportamiento periódico o
cíclico, mientras que trayectorias al otro lado podrían converger hacia un
estado de reposo. Más
aún, en el proceso de separar distintas regiones del espacio
de estados, estas superficies pueden llegar a producir impresionantes formas geométricas,
lo cual hace aún más intrigante su estudio. Por ejemplo:
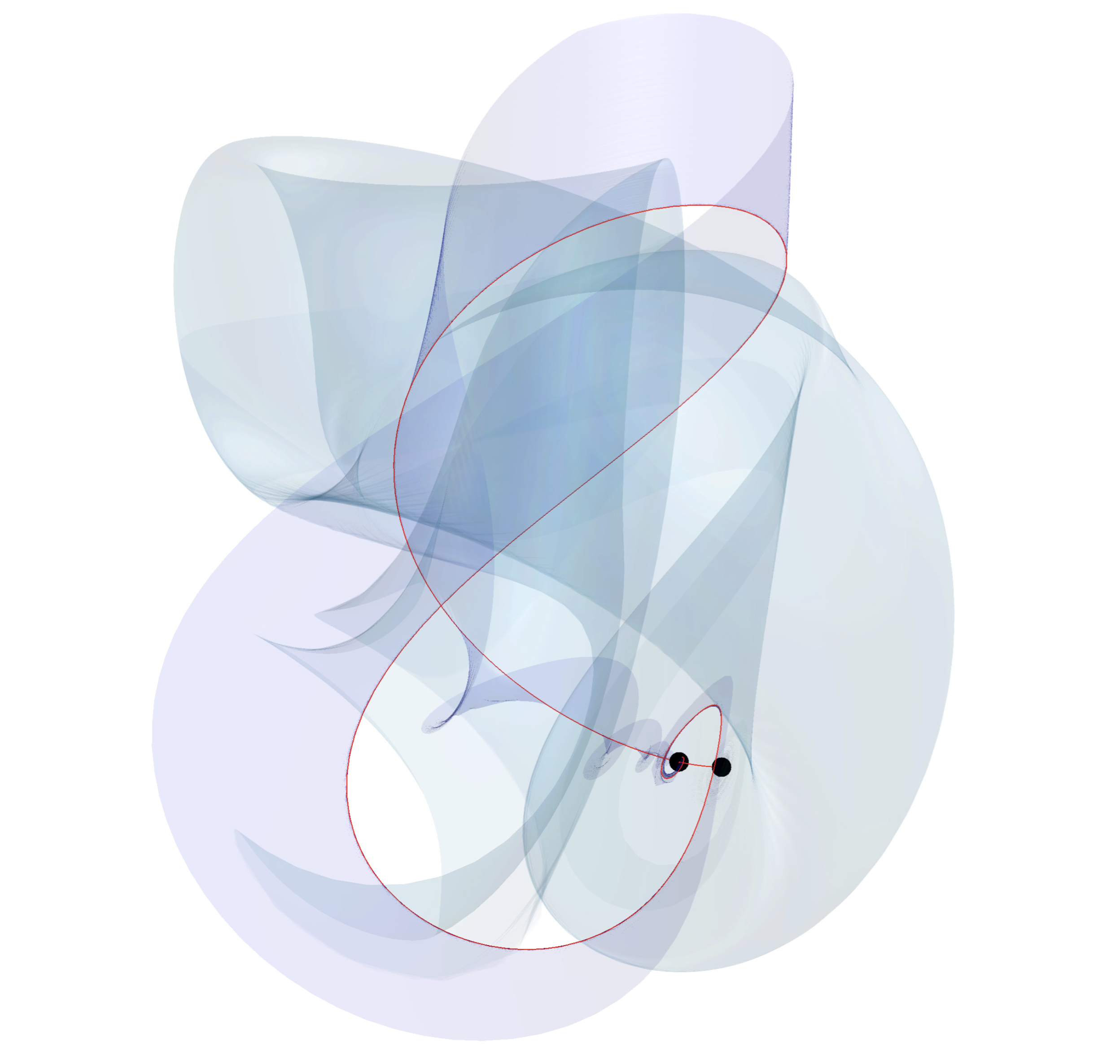 Variedades invariantes
cerca de una bifurcación silla-nodo homoclínica de codimensión
2.
Variedades invariantes
cerca de una bifurcación silla-nodo homoclínica de codimensión
2.
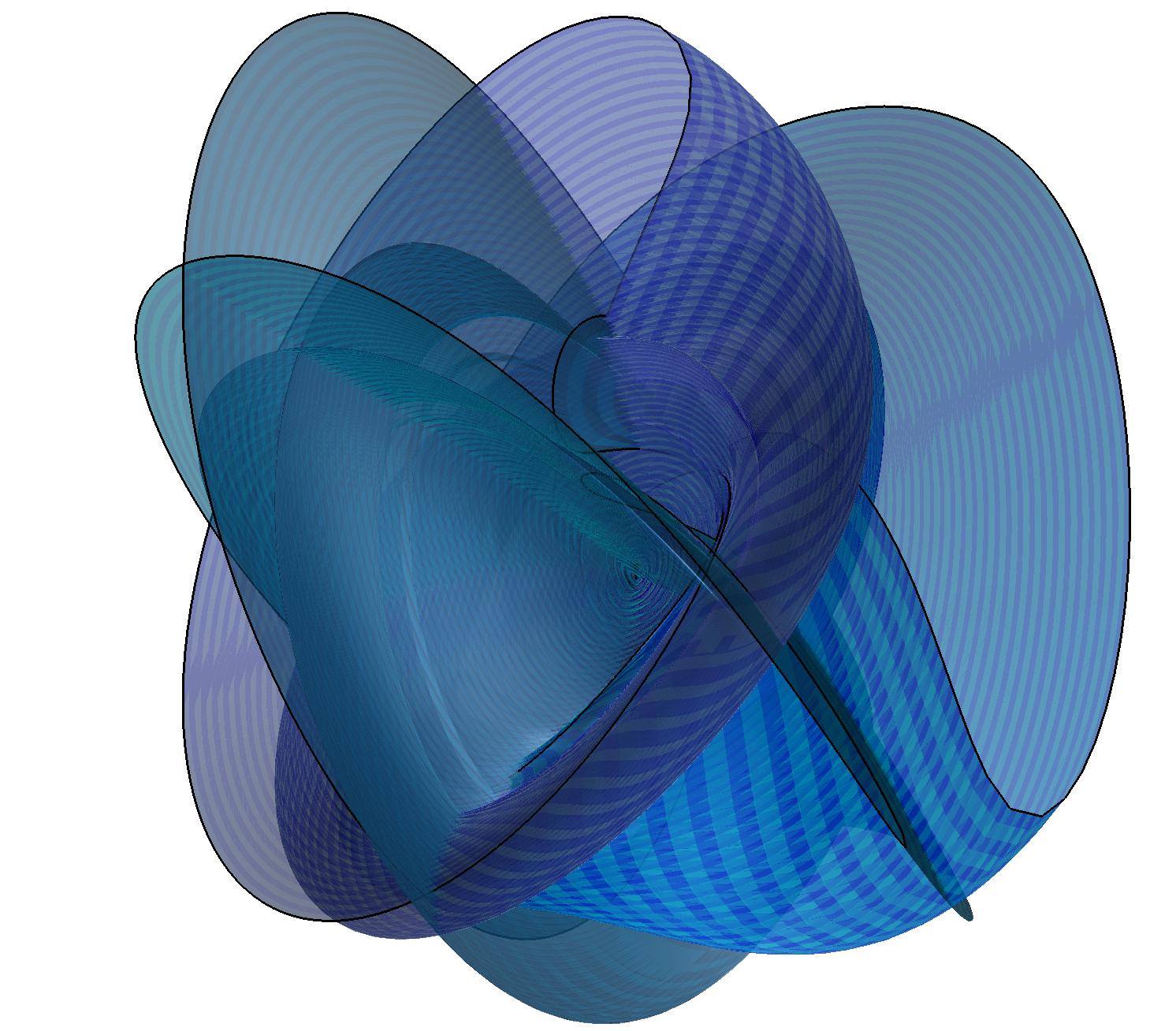 Variedades invariantes en el modelo de
Swift-Hohenberg, definido por un campo de vectores en 4D.
Variedades invariantes en el modelo de
Swift-Hohenberg, definido por un campo de vectores en 4D.
Puedes ver también algunos
ejemplos en la Galería Multimedia del portal DSWeb (https://dsweb.siam.org/Media-Gallery/orientable-and-non-orientable-invariant-manifolds), manejado por el SIAM
Activity Group on Dynamical Systems.
Típicamente, estas
superficies pasan por cambios cuando el sistema sufre
perturbaciones. Estos cambios se llaman bifurcaciones. Estas
bifurcaciones pueden tener un efecto dramático en la
configuración de las variedades invariantes y, por lo tanto,
en la organización general del espacio de estados, creando (o
destruyendo) cuencas de atracción y dando origen a
comportamientos complejos incluyendo caos. Esto es de especial
interés para entender la naturaleza de sistemas que sufren
bifurcaciones globales como en dinámica de lásers, impulsos
nerviosos en las neuronas, reacciones electroquímicas,
sistemas de comunicación basados en caos, cadenas alimenticias
en modelos de poblaciones, etc.
De esta manera, buscamos
responder las siguientes preguntas: ¿Cómo cambian las
variedades invariantes topológica y geométricamente durante
una bifurcación dada? ¿Cuáles son los mecanismos de
bifurcación que producen dinámica caótica en un modelo dado?
¿Y cómo esto afecta la organización de un sistema dinámico? En
particular, ¿Cuáles son las posibles interpretaciones de estas
rutas al caos en el contexto de un modelo aplicado concreto?
Para responder estas preguntas, utilizamos herramientas
analíticas de la teoría de sistemas dinámicos en combinación
con avanzados métodos numéricos para el cálculo preciso de
variedades invariantes. De esta forma, somos capaces de
explicar cómo ciertas bifurcaciones globales de interés pueden
provocar cambios dramáticos en la dinámica.
Algunos temas específicos de
interés son:
- Bifurcaciones de variedades invariantes globales y
métodos computacionales asociados
- La dinámica y propagación de enfermedades infecciosas
- Cuencas de atracción y dinámica global en modelos
poblacionales
- Modelación y estudio de la organización de bacterias
mediante señales moleculares o quemotaxis
- Mecanismos matemáticos de excitabilidad y caos en modelos
neuronales
- Propiedades fractales de variedades invariantes de
conjuntos caóticos en bifurcaciones homoclínicas
Research Grants and Projects
Ongoing Projects
- STIC AMSUD230013
(Coodinador Responsable
Nacional), 2024-2025. Proyecto de investigación y
colaboración internacional BIO-CIVIP
- BIOlogical Control of Insect Vectors and Insect Pests.
- Proyecto Interno UTFSM
PI_LIR_24_04 (Investigador Principal),
2024-2025. Umbrales epidemiológicos y estrategias de
contención de enfermedades infecciosas.
Finished Projects
- Concurso Subvención a la
Instalación en la Academia PAI77180076 (Investigador
Patrocinante), 2019-2021. Programa de Atracción e
Inserción de Capital Humano Avanzado PAI-CONICYT. Proyecto de investigación Del orden al caos: Descifrando
sistemas dinámicos y sus aplicaciones en múltiples escalas de
tiempo. Investigador Principal: José Pablo Mujica.
- Proyecto Interno UTFSM
PI_LI_19_06 (Investigador Principal), 2019-2021. Bifurcaciones de variedades
invariantes: Teoría y aplicaciones.
- CONICYT Redes 17009 (Investigador Asociado),
2018-2019. Proyecto de investigación y colaboración
internacional AM2V-MobiMat
network on modeling and control of communicable and infectious
diseases.
- MATH-AmSud-Conicyt 18MATH-05
(Investigador Asociado),
2018-2019. Proyecto de investigación y colaboración
internacional Modeling,
Optimization and Viability for Epidemics Control (MOVECO).
- Fondecyt Iniciación 11150306
(Investigador Principal),
Fondecyt-Conicyt, 2015-2018. Proyecto de investigación Global bifurcations and invariant
manifolds: From simple to chaotic dynamics.
- STIC-AmSud-Conicyt 16STIC-02
(Coordinador Responsable
Nacional), 2016-2018. Proyecto de investigación y
colaboración internacional MOSTICAW-Modeling
the Spread and (opTImal) Control of Arviroses by Wolbachia.
- Proyecto Interno
Multidisciplinario DGIP-USM 216.22.2 (Co-investigador),
2016-2018, UTFSM. Estudio de
las propiedades fractales de árboles eléctricos y de la
dinámica de las descargas parciales involucradas en la
degradación de aislamientos eléctricos.
- FONIS SA15|20311
(Co-investigador), Diciembre 2015-Diciembre 2017,
Universidad del Desarrollo. Fondo Nacional de Investigación y
Desarrollo en Salud, Conicyt. Proyecto de investigación Costo efectividad del test rápido
para la detección de enfermedades infecciosas en población
privada de libertad: Sífilis.
- Fondecyt Regular 1151441
(Co-investigador), Programa Fondecyt-Conicyt,
2015-2018. Proyecto de investigación Statistical and mathematical modelling as a knowledge
bridge between Society and Ecological sustainability.
- Fondecyt Postdoctorado
3130497 (Investigador Principal), Fondecyt-Conicyt,
2012- 2015. Proyecto de investigación Global dynamics and bifurcations: Insight into theory
and applications.
- Anillo ACT 1103 Center
of Dynamical Systems and Related Fields (Inv. Asociado),
Conicyt, 2012-2015.
- Proyecto Interno DGIP-USM
12.13.10 (Investigador Asociado), 2013-2014, UTFSM. Asymptotic analysis of perturbed
dynamical systems and applications.

See also: Publications.

Universidad Técnica Federico
Santa María / Departamento de
Matemática /
P Aguirre
 Variedades invariantes
cerca de una bifurcación silla-nodo homoclínica de codimensión
2.
Variedades invariantes
cerca de una bifurcación silla-nodo homoclínica de codimensión
2. Variedades invariantes
cerca de una bifurcación silla-nodo homoclínica de codimensión
2.
Variedades invariantes
cerca de una bifurcación silla-nodo homoclínica de codimensión
2. Variedades invariantes en el modelo de
Swift-Hohenberg, definido por un campo de vectores en 4D.
Variedades invariantes en el modelo de
Swift-Hohenberg, definido por un campo de vectores en 4D.
